Для подробного ознакомления с медицинской и исследовательской техникой основных мировых производителей оптических систем и сопутствующего оборудования посетите наш каталог или свяжитесь с нашими специалистами и получите полную профессиональную консультацию по любым, имеющимся у Вас, вопросам.
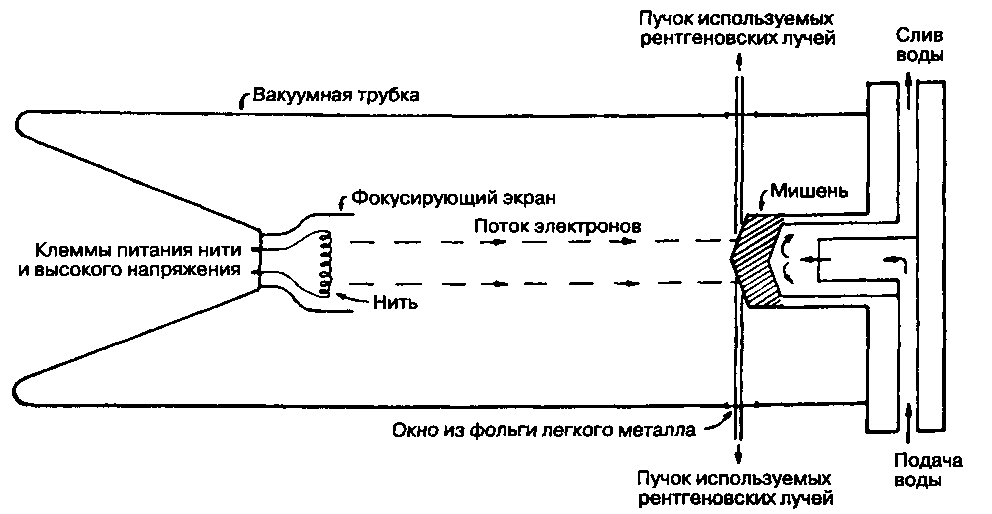
Рис. 4.3 Схема рентгеновской трубки
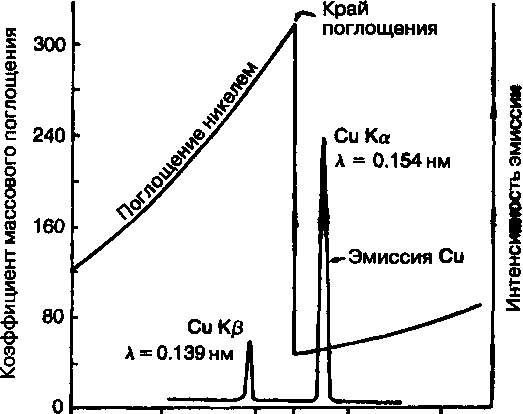
Рис. 4.4 Взаимоотношение между краем поглощения никеля и эмиссионным спектром меди
Поэтому точно так же, как свет дифрагирует на решетке с очень близко расположенными линиями, так и рентгеновские лучи рассеиваются атомами, слагающими трехмерное пространство кристаллической решетки. При дифракции света каждое отверстие в решетке функционирует как новый источник лучей. Аналогичным образом каждое электронное облако в атомах кристалла рассеивает рентгеновские лучи и действует, как источник вторичных лучей с той же самой длиной волны. В 1912 г. У. Л. Брэгг показал, что в такой ситуации рентгеновские лучи ведут себя точно так же, как если бы они отражались от плоскостей, содержащих атомы, которые слагают кристаллическую структуру. Следовательно, все эти вопросы можно рассматривать с использованием более известных терминов, касающихся отражений от плоскостей, а в таком случае анализ существенно упрощается.
<б)
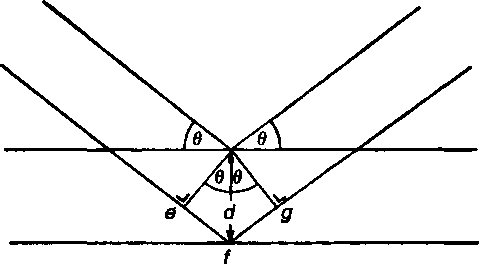
(а) условие отражения, (6) разность хода лучей
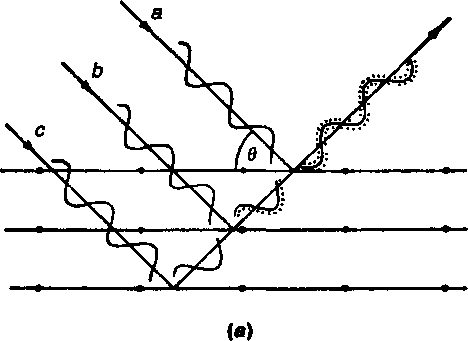
Рис. 4.5 Брэгговский угол отражения: = 2dsinq.
Представим себе систему атомных плоскостей (рис. 4.5) и пучок рентгеновских лучей, бомбардирующий их под углом q. Лучи не только пронизывают слои сеток, но и отражаются ими. На первой плоскости отражается луч о, на второй — луч Ъ. Лучи, отраженные от всей серии плоскостей, приобретают одинаковое направление, и если они находятся в противофазе, то, интерферируя между собой, будут гасить друг друга. Только в том случае, когда разница в длине пути лучей, отраженных от последовательных плоскостей, составляет четное число длин волн, они будут способны усиливать друг друга и образуют устойчивый ряд отраженных лучей. На рис. 4.5,б можно видеть, что лучи, отраженные от последовательных плоскостей, будут иметь разность хода ef + fg. Затем можно записать: ef = fg = dsinq, где d — расстояние по перпендикуляру между плоскостями. Итак, условие успешного отражения задается уравнением Брэгга—Вульфа
Из уравнения Брэгга—Вульфа видно, что семейство плоскостей, расположенных на одном и том же определенном расстоянии друг от друга, может отражать рентгеновские лучи заданной длины волны только под одним углом, равным углу падения.
Уравнение Брэгга—Вульфа используется для нахождения межплоскостных расстояний в кристалле. Как мы видели, рентгеновские лучи известной длины волны можно получить с помощью подходящей мишени и соответствующего фильтра. Угловые позиции отраженных лучей по отношению к исходному направлению неотклоненного пучка фиксируются на фотопленке или электронным рентгеновским детектором. В рентгеновских камерах фотопленка помещается вокруг исследуемого кристалла или перед ним в зависимости от конкретного типа камеры. Пленка засвечивается в тех местах, где на нее попадает отраженный пучок (см. рис. 4.6, а также рис. 4.15 и 4.16). Угол между прямым или неотклоненным пучком и отраженным пучком составляет 20. В современной кристаллографии для записи угла 2q между падающим и отраженным пучками обычно применяются дифрактометры, в которых используются электронные детекторы. Зная X и q, полученные при дифракционных исследованиях, можно рассчитать d.
Отсутствие отражений
Отражения для всех возможных значений hkl могут наблюдаться только в том случае, когда решетка является примитивной и симметрия кристалла не включает трансляционных элементов (плоскостей скольжения или винтовых осей). Если решетка представлена гране- или объемноцентрированным типом, то семейства плоскостей с некоторыми индексами не содержат всех узлов решетки. Для примера на рис. 4.17 приведена в плане базоцентрированная ромбическая решетка с нанесенными на ней следами некоторых характерных семейств плоскостей. Показано, что семейства, расположенные с левой стороны диаграммы, содержат все узлы решетки, тогда как у расположенных с правой стороны центральный узел на С-грани отсутствует. Устойчивые отражения не образуются от семейства плоскостей, у которых нет центральных узлов, так как отсутствующие и имеющиеся узлы совместно образуют параллельные семейства плоскостей с межплоскостным расстоянием, равным половине d, как это показано на рисунке. Эти меньшие чем d межплоскостные расстояния вполне удовлетворяют уравнению Брэгга—Вульфа. Ряды с большими межплоскостными расстояниями не могут давать собственных отражений в связи с тем, что они будут гаситься другими отражениями (отличающимися по фазе на 1 /2l) от плоскостей с половинным расстоянием между узлами решетки, не находящимися с ними в одной фазе.
В рассматриваемом случае требование, чтобы семейство плоскостей содержало все узлы решетки, удовлетворяется, когда значение (h + к) представлено четным числом. Если (h + к) нечетное, то центральные узлы отсутствуют и никаких отражений не возникает.
Этот принцип можно обобщить в ряд правил, которые сведены в приводимую ниже таблицу и позволяют идентифицировать тип решетки по сочетанию чисел индекса, устанавливаемых на основе дифракционной картины. В тех случаях, когда необходимые ограничения не удовлетворяются, отражения будут систематически отсутствовать.
На рис. 4.18 схематически показано влияние на порошковую дифрактограмму систематического отсутствия отражений, что обусловлено типом решетки кубических элементарных ячеек.

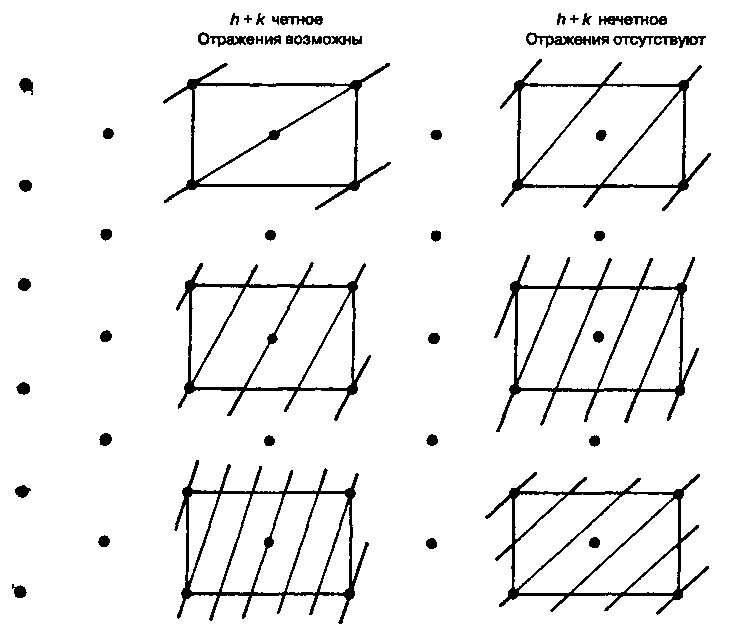
Рис. 4.17 Отсутствие отражений
Кроме того, систематическое отсутствие отражений связано с трансляционными элементами симметрии — плоскостями скольжения и винтовыми осями. Но отражения возникают вновь, когда распределение атомов, объединенных этими операторами симметрии, таково, что отражения от некоторых рядов плоскостей будут иметь разность фаз, равную 1/2l, и поэтому их интенсивность будет равняться нулю. Полные табличные данные систематического отсутствия отражений, связанного с операторами трансляционной симметрии, содержатся в некоторых публикациях, приведенных в конце главы.
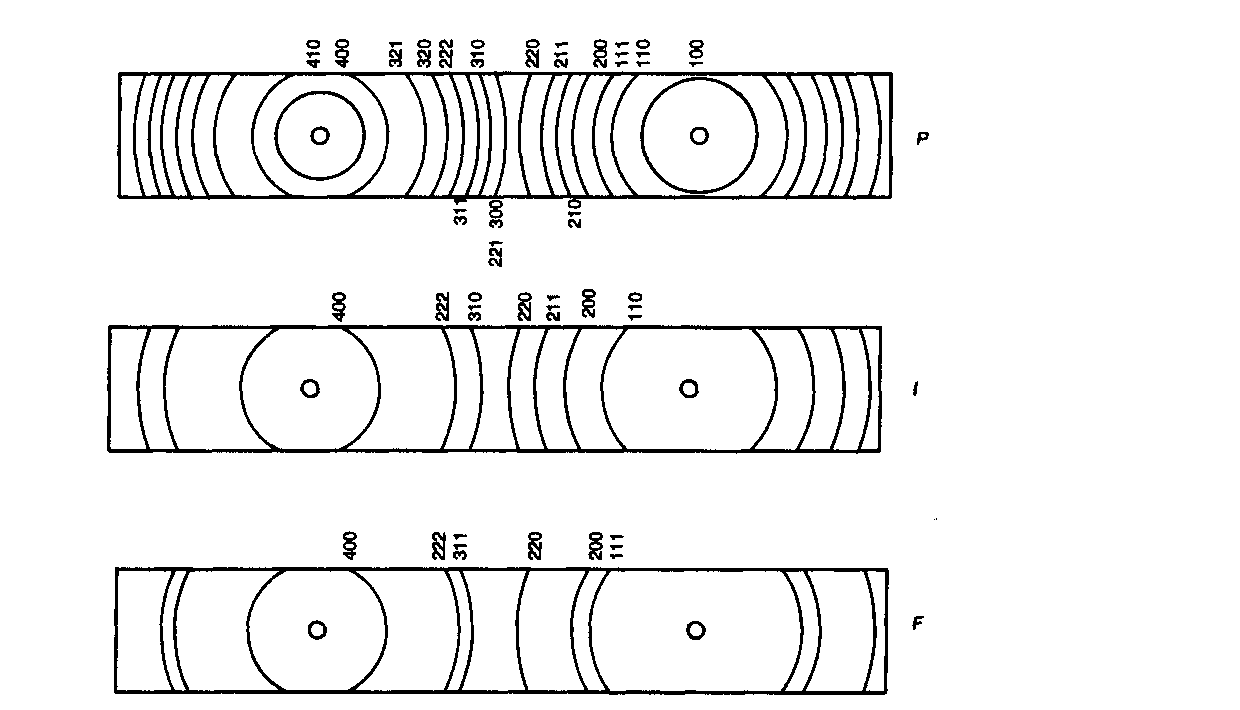
Рис. 4.18 Порошковая дифрактограмма (Со Ka излучение с X = 0,179026 нм) кубического кристалла с а = 0,375 нм, иллюстрирующая систематическое отсутствие отражений, связанное с типом решетки. Вверху — примитивная решетка (P): возможны все значения h, k и /; в середине — объемноцентрированная решетка (I): отражения возникают только в том случае, когда сумма h + k +l является четным числом; внизу — гранецентрированная решетка (F): h, k и l должны быть все четные или все нечетные
Дифракция нейтронов
Нейтроны могут рассеиваться атомными плоскостями кристалла, и поэтому их можно использовать для определения кристаллической структуры. Однако в отличие от рентгеновских лучей и электронов, которые рассеиваются электронами, рассеяние нейтронов вызывается ядрами атомов. В то время как рассеяние рентгеновских лучей связано с атомным номером, рассеяние нейтронов такой связи не обнаруживает. Дифракция нейтронов позволяет распознавать атомы с близкими атомными номерами, например такие, как Si и Al. Следовательно, ее можно использовать для определения степени упорядочения решетки в тетраэдрических узлах силикатов, а также для обнаружения легких элементов, таких, как H и Li, выявить которые традиционными методами рентгеновской дифракции бывает затруднительно. Поскольку нейтроны взаимодействуют и с неспаренными электронами в кристаллах, то дифракция нейтронов применяется также для изучения магнитной упорядоченности в минералах. Исследования методами порошковой дифракции и дифракции в монокристаллах можно проводить с использованием нейтронов. Но имеются два важных ограничения, которые препятствуют их широкому применению в минералогии. Первое ограничение связано с тем фактом, что пучок нейтронов, как правило, маломощен (т. е. обладает слабым потоком) и поэтому для исследования необходимо иметь значительно большие количества материала, чем при дифракции рентгеновских лучей — требуется монокристалл с ребром в несколько миллиметров или порошок массой в несколько граммов. Другое важное ограничение состоит в том, что в большом количестве нейтроны генерируются лишь в ядерных реакторах, и поэтому исследования с использованием нейтронов могут проводиться только на специальных ядерных установках.
Дифракция электронов и просвечивающий электронный микроскоп
Электроны, подобно рентгеновским лучам и нейтронам, характеризуются длиной волны, и поэтому атомные плоскости в кристалле почти точно так же рассеивают и их. Электронные дифракционные картины получаются с помощью просвечивающего (трансмиссионного) электронного микроскопа (ПЭМ). При этом длины волн ускоренных электронов зависят от разности потенциалов между катодом и анодом. У типичного ПЭМ, имеющего ускоряющий потенциал 100 или 200 кВ, длины волн электронов в пучке составляют соответственно 0,0037 и 0,0025 HM, т. е. они приблизительно в 50-100 раз меньше, чем длины волн рентгеновских лучей. Вследствие этого при дифракции электронов брэгговские углы в гораздо меньше, и поэтому удается получать электронные дифракционные картины, подобные прецессионным фотографиям монокристаллов. При этом нет необходимости вращать кристалл в электронном пучке или передвигать пленку (рис. 4.19).
Имеются и другие различия между дифракцией электронов и рентгеновских лучей. Электроны, как и рентгеновские лучи, рассеиваются электронными облаками атомов, находящихся в кристаллографических плоскостях, но приблизительно в 100 раз интенсивнее, чем рентгеновские лучи. Это позволяет исследовать гораздо более мелкие фрагменты кристалла и облегчает изучение таких слабых дифракционных эффектов, какие возникают при некоторых формах упорядочения атомов. Главное различие, однако, состоит в том, что электроны в отличие от рентгеновских лучей могут фокусироваться магнитными линзами, что позволяет с легкостью получать изображения на ПЭМ.

Рис. 4.19 Электронная дифракционная картина галенита PbS вдоль четверной оси.
Существует много общего в процессе получения изображения на ПЭМ и обычном поляризационном микроскопе. На рис. 4.20 приведены схематические чертежи этих двух типов микроскопов. Заметим, что на этом рисунке поляризационный микроскоп изображен в перевернутом виде — источник освещения находится вверху, а не внизу.
У ПЭМ источником электронов является нить электронной пушки. Электроны образуются при прохождении через нить сильного электрического тока и ускоряются за счет разности потенциалов между катодом и анодом. Затем пучок электронов проходит через ряд электромагнитных линз, составляющих конденсорную линзовую систему, которая фокусирует электроны в четко ограниченный пучок. После этого пучок проходит через образец и электроны рассеиваются атомными плоскостями. На следующем этапе дифрагированный электронный пучок проходит через линзы объектива. Электронная дифракционная картина образуется на тыловой фокальной плоскости линзы объектива. Это в какой-то степени аналогично тому, что происходит при рассмотрении оптических фигур с линзами Бертрана (см. разд. 7.8.5). Затем пучок проходит через систему промежуточных и проекционных линз, которая служит для увеличения изображения и проецирования его на экран прямого видения. Электромагнитные линзы системы промежуточных и проекционных линз могут быть настроены таким образом, что на экран прямого видения будет проецироваться или электронная дифракционная картина, или увеличенное изображение образца. Чтобы электроны в пучке не рассеивались атомами и молекулами воздуха, в колонне микроскопа необходимо создать очень высокий вакуум. Для изучения на ПЭМ образцы должны быть очень тонкими (менее 1 мкм), а для создания высокого разрешения в тех случах, когда получается непосредственное изображение кристаллической структуры, нужно иметь образцы толщиной меньше 10 HM. Для исследований на ПЭМ образцы можно изготовить путем раздавливания и растирания минералов или другими методами измельчения, которые позволяют довести до требуемой толщины участки обычных петрографических шлифов.
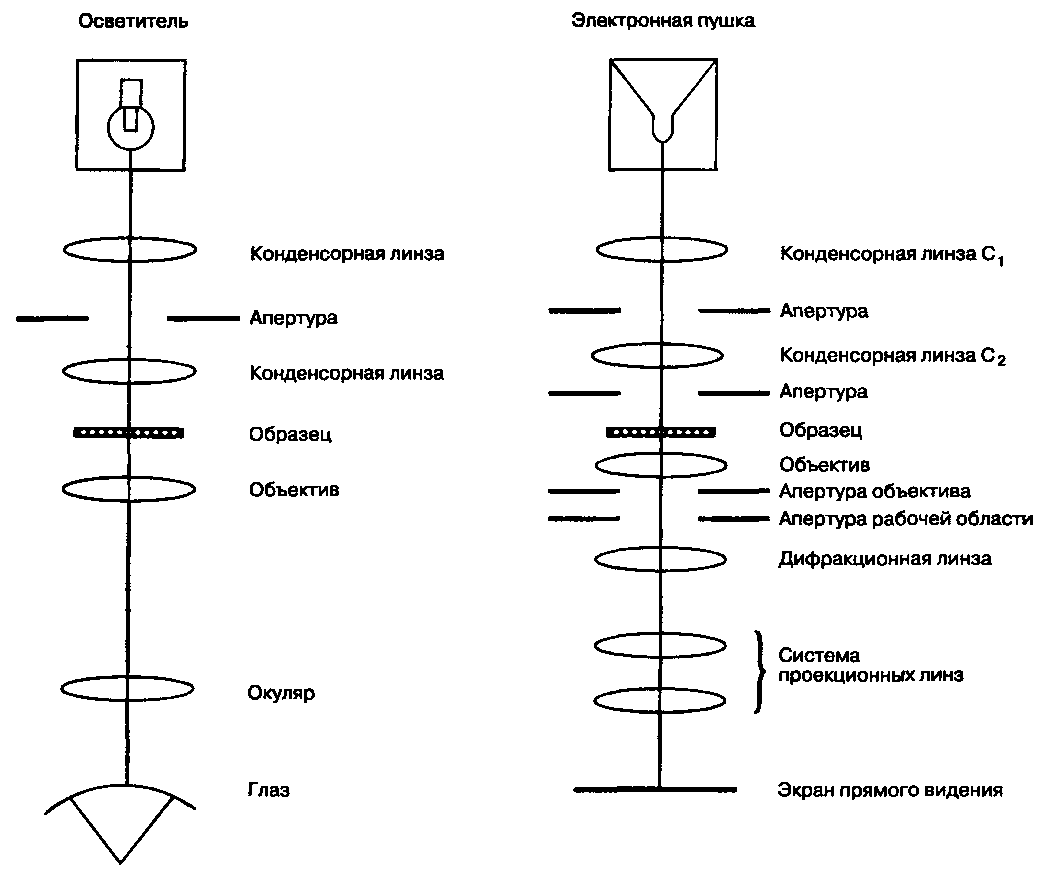
Рис. 4.20 Схемы поляризационного микроскопа (слева) и просвечивающего электронного микроскопа (справа). На этом чертеже поляризационный микроскоп изображен в перевернутом виде — источник освещения находится не снизу, а сверху.
Изображения, получаемые на ПЭМ
Будучи инструментом современной минералогии, ПЭМ дает возможность исследовать минералы множеством различных способов и поставляет информацию о структурных взаимоотношениях, которую трудно получить другими методами.
Высокая разрешающая способность при получении структурных изображений
Разрешающая способность поляризационных микроскопов зависит от длины волны света. А у современных ПЭМ она ограничивается не длиной волны используемых электронов, а оптическими характеристиками электромагнитных линз и другими инструментальными факторами. Электронные микроскопы, приспособленные для воспроизведения изображений с высоким разрешением, дают прямые картины структур или кристаллических решеток с разрешением между 0,15 и 0,25 HM (рис. 4.21). Изображение решетки с высоким разрешением позволяет непосредственно наблюдать пространственное расположение атомов в минералах, но при этом не достигается такая точность измерений структур, которую можно получить при использовании рентгеновской дифракции на монокристаллах. Поэтому данный метод применяется преимущественно тогда, когда отсутствуют монокристаллы необходимого для рентгенографии размера. С его помощью можно также проследить ход полиморфных фазовых переходов и реакций между минералами на атомном уровне (рис. 4.22).
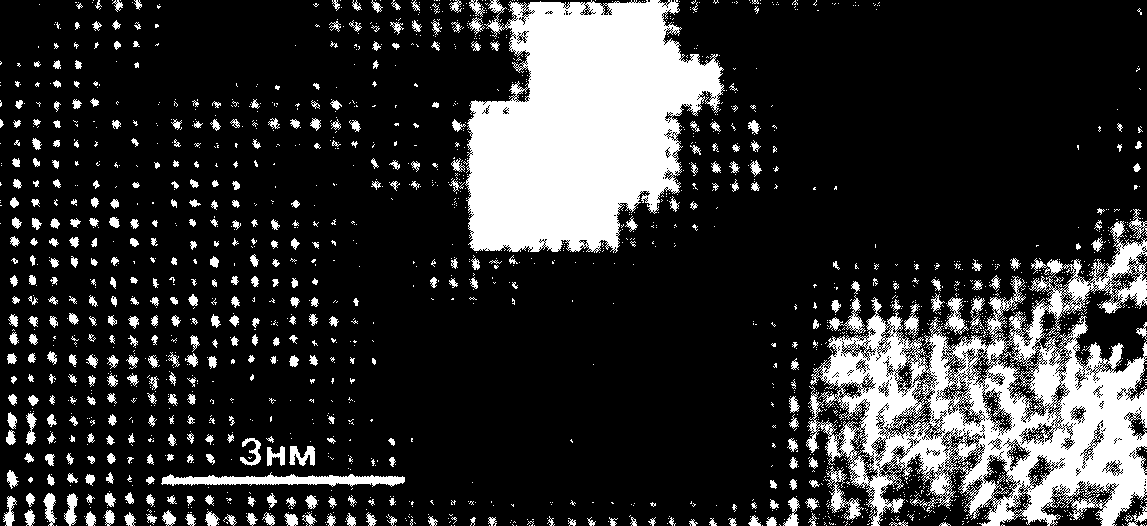
Рис 4.21 Выполненная на просвечивающем электронном микроскопе с высокой разрешающей способностью микрофотография структуры галенита вдоль четверной оси В нижнем правом углу приведено изображение ребра кристалла Там же можно видеть изменения в изображении деталей при увеличении толщины препарата

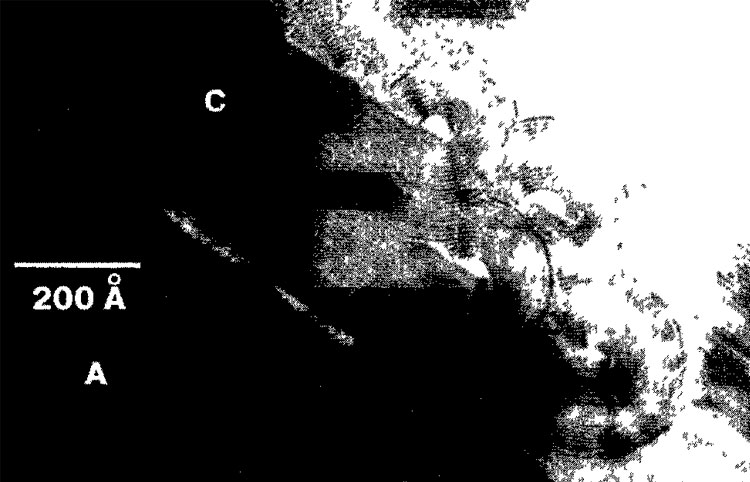
Рис 4.22 Микрофотография, выполненная на ПЭМ с высоким разрешением и показывающая взаимопрорастание лизардита — минерала из группы серпентина (С) и талька (T) в кристалле амфибола (А) Заметим, что концы серпентиновых слоев завернуты в обратную сторону, образуя цилиндрические формы

Рис. 4.23 Электронная микрофотография, показывающая экссолюционные пластинки альбита в криптопертите. Отметим двойникование в альбитовых пластинах, связанное со сменой моноклинной фазы на триклинную, которая произошла при охлаждении уже после распада твердого раствора

Рис. 4 24 Электронная микрофотография, показывающая двойникование альбита и экссолюцию пластинок калиевого полевого шпата в анортоклазе (Ab75Or20An5) с горы Франклин пров Виктория (Австралия) Заметим, что двойникование альбита предшествует распаду калиевого полевого шпата
Получение контрастного изображения с помощью дифрагированных пучков
В то время как при получении изображения решетки с высоким разрешением большинство дифрагированных пучков (или все они) для образования изображения воссоединяются в тыловой фокальной плоскости линзы объектива, при контрастном изображении число дифрагированных пучков, участвующее в формировании изображения, ограничивается посредством введения апертуры в тыловую фокальную плоскость линзы объектива. Следовательно, изображение можно получать путем отбора только одного или двух пучков—центрального недифрагированного пучка и одного или нескольких подвергшихся дифракции.
При этом образуется, хотя и с гораздо более низким разрешением (обычно 0,5-2,0 HM), изображение, позволяющее изучать в деталях такие объекты, как кристаллографические дефекты, мельчайшие продукты распада твердого раствора, двойники, а также взаимное прорастание минеральных фаз. С помощью контрастного изображения была выявлена тонкая микроструктура полевых шпатов и пироксенов, что позволило исследователям лучше понять кристаллохимию и термическую историю этих минералов в различных породах (рис. 4.23 и 4.24).