Некоторые стереограммы, приведенные на рис. 3.37, свидетельствуют о том, что если для исходного полюса грани общей основной формы кристалла выбрать какое-либо иное положение, то оператор симметрии будет образовывать новые геометрические тела, хотя и сходные, но все же отличающиеся морфологически. При этом возможны два случая.
Для подробного ознакомления с медицинской и исследовательской техникой основных мировых производителей оптических систем и сопутствующего оборудования посетите наш каталог или свяжитесь с нашими специалистами и получите полную профессиональную консультацию по любым, имеющимся у Вас, вопросам.
Дополнительные формы
В классе тЗ (= 2/тЗ) исходный полюс может быть помещен или в точку А, или в точку В (рис. 3.45). На рисунке приведены две соответствующие стереограммы и геометрические тела, которые они представляют. Из стереограмм видно, что эти тела связаны посредством поворота на 90°. В совокупности они образуют все грани голоэдрического класса m3m и поэтому называются дополнительными формами. Между ними имеется некоторое различие, так как для любой заданной ориентации внутренней сетки атомов связь между гранями выбранной формы А и пространственным расположением ее атомов отлична от той, которая наблюдается в случае В.
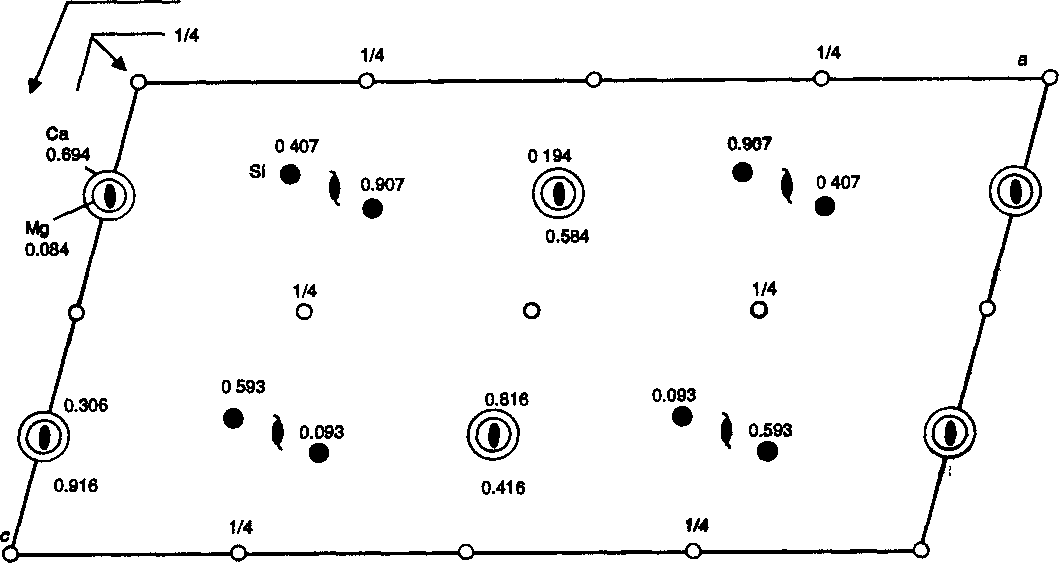
Рис. 3.44 Вид элементарной ячейки диопсида, где ось у уходит за пределы страницы. Показаны уровни расположения катионов и операторы симметрии. Положения атомов кислорода не указаны для упрощения схемы.
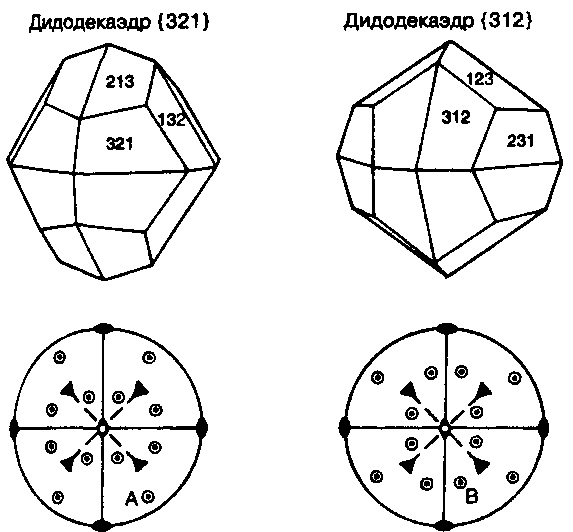
Рис. 3.45 Дополнительные формы
Эти две выбранные формы часто определяют как «положительные» и «отрицательные», и в данном случае следует говорить о «положительном» и «отрицательном» дидодекаэдрах. Иногда вместо этих терминов говорят просто: «положительная» форма, подразумевая, что имеется исходный полюс грани в октанте стереограммы, где все индексы положительны. В других случаях выбор названий для простой формы менее очевиден (примером может опять-таки служить дидодекаэдр), и тогда, возможно, наиболее легким выходом является определение простой формы через ее индексы. Например, на рис. 3.45 левый дидодекаэдр обозначается {321}, а правый — {312}. Существует также вероятность путаницы «положительных» и «отрицательных» форм минералов с их соответствующими оптическими знаками. Именно поэтому словесные описания простых форм даются здесь в кавычках.
Энантиоморфизм
На рис. 3.46 показан другой вид взаимоотношений в 32-м классе кристаллов. У нас имеется выбор в размещении на стереограмме исходного полюса грани общей простой формы (наподобие {5161}), и на рисунке показаны два возможных варианта. Как видно, левая стереограмма не может быть переориентирована таким образом, чтобы она оказалась идентичной правой, и, конечно, то же самое относится и к геометрическим телам, помещенным над стереограммами. Обе выбранные формы соотносятся между собой таким же образом, как правая и левая перчатки: они не могут быть точно совмещены при наложении друг на друга. Такие формы называются энантиоморфными. Соответствующие им кристаллы обладают способностью вращать плоскости поляризации поляризованного света и различаются как левосторонние и правосторонние в зависимости от того, в какую сторону они вращают эту плоскость (с точки зрения наблюдателя, смотрящего через кристалл в направлении источника света). Для иллюстрации сказанного нами выбран низкотемпературный кварц (класс 32) — один из наиболее интересных случаев энантиоморфизма. В низкотемпературном кварце развиты дополнительные формы (грани ромбоэдров r и z на рисунке), и потому семейство этой общей формы объединяет четыре члена: «положительные» и «отрицательные» правосторонние и «положительные» и «отрицательные» левосторонние. Спиральное соединение тетраэдров SiO4 в структуре кварца, показанное на рис. 2.15, коррелируется с его оптическими свойствами.
Энантиоморфизм проявляется во многих органических соединениях и даже сохраняется при их переходе в раствор. Сохраняющаяся при этом в растворенном состоянии право- и левовращающая способность позволяет распознавать исходные соединения.
По своей природе Энантиоморфизм может проявляться лишь тогда, когда в структуре не имеется ни плоскости симметрии, ни какого-либо воздействия инверсии. Следовательно, он существует только в классах (или пространственных группах), у которых единственными элементами симметрии являются поворотные (и винтовые) оси. К таким, не обладающим центрами симметрии классам, относятся:
1 триклинный
моноклинный
222 ромбический
3,32 тригональный'
23,43 кубический
4,42 тетрагональный
6,62 гексагональный
Отнесение какого-либо минерала к имеющему или не имеющему центр симметрии может оказаться непростой задачей. Свидетельства о присутствии или отсутствии центра симметрии иногда можно получить, основываясь на данных морфологии кристаллов и их способности вращать плоскость поляризации света.
Фигуры травления, пьезо- и пироэлектричество
Истинная симметрия иногда может проявляться в виде природных знаков на гранях кристаллов. Это часто встречается у пирита (класс тЗ), кубические кристаллы которого несут штриховку на гранях, образовавшихся в процессе развития плоскостей, отличных от {100}. Направление штриховатости позволяет объединить в три пары противоположные грани куба. Это свидетельствует о том, что основные оси обладают двойной, а не четверной симметрией (рис. 3.47).
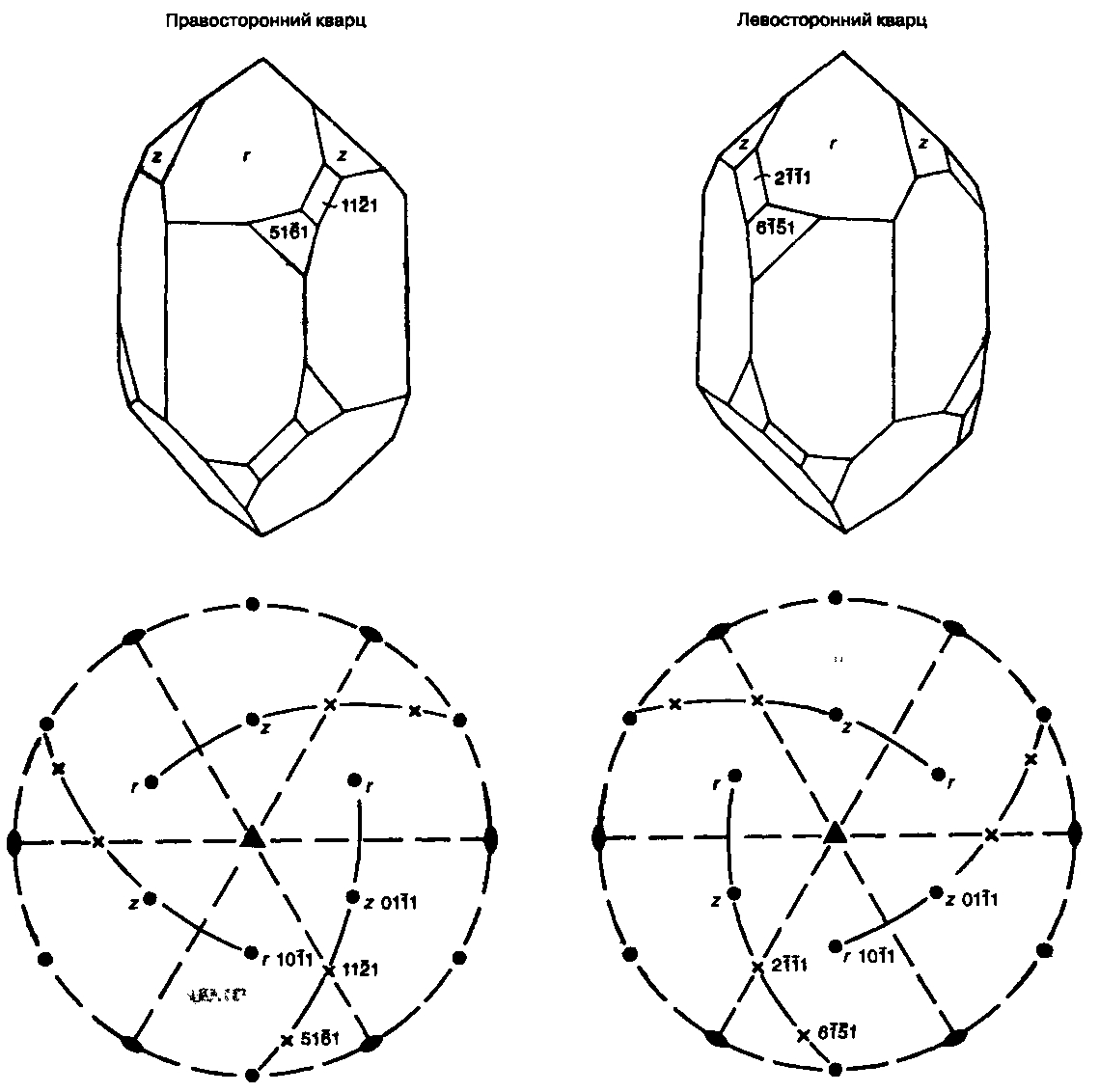
Рис. 3.46 Кварц как пример энантиоморфизма в минералах.
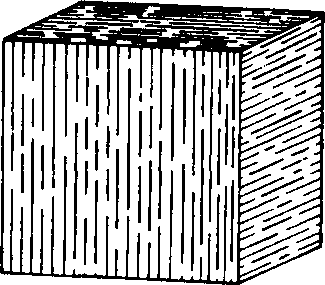
Рис 3.47 Куб пирита со штриховкой на гранях
В других случаях группы граней, которые представляются принадлежащими к высшей симметрии, могут быть разбиты на два или большее число отдельных видов по форме и ориентации ямок травления, называемых фигурами травления. Последние можно получить в результате воздействия на грани соответствующих растворителей—минеральных кислот, едких щелочей или фтористоводородной кислоты. Скорость растворения кристалла часто различается вдоль различных направлений, что связано с внутренним пространственным расположением атомов. Ориентация образующихся угловатых ямок может дать ключ к пониманию симметрии или служить средством для распознавания право- и левосторонних форм. Примеры подобных отличий даются при описании отдельных минералов.
Пьезоэлектричество и пироэлектричество представляют собой взаимосвязанные явления, возникающие в тех случаях, когда давление или тепловое воздействие, соответственно, приводят к появлению электрических зарядов на поверхности кристаллов. Эти свойства подробнее рассматриваются в гл. 6. Здесь важно отметить, что они проявляются только в тех кристаллах, которые не имеют центра симметрии.
Двойникование
Благодаря симметрии кристаллической структуры появляется возможность роста сдвойникованных кристаллов. Сдвойникованный кристалл морфологически представляет собой единое тело, состоящее из двух (или большего числа) индивидов, причем один из них может находиться в обратной структурной ориентации относительно другого. В таких кристаллах обращенную ориентацию имеет ряд плоскостей решетки, причем прочность сцепления между ними не ослаблена. Двойниковый рост может происходить тогда, когда группы атомов расположены таким образом, что с одинаковым успехом образуют фрагменты решетки по любую сторону от плоскости, на которой происходила смена ориентации. Если при поступлении атомов к растущему кристаллу создается возможность подобной смены направления кристаллизации, то последующие слои атомов присоединяются в иной ориентации, в результате чего и будет формироваться сдвойникованный кристалл (двойник).
Сразу же должно быть очевидно, что переориентация решетки осуществляется не через плоскость симметрии, так как при образовании двойников создаются условия для возникновения симметрии отражения через плоскость срастания. Если же такая симметрия уже существовала, то никаких изменений в ориентации не должно наблюдаться. Подчеркнем, что операция симметрии эквивалентна вращению решетки вокруг оси, перпендикулярной плоскости срастания двойников и, следовательно, никакой двойной оси или другой поворотной оси четной степени, которая также перпендикулярна к этой плоскости, присутствовать не может. Однако не исключена возможность существования тройной оси, перпендикулярной указанной плоскости.
Во внешней форме кристалла двойникование часто обнаруживается по присутствию входящего угла между гранями (рис. 3.48), который обычно не встречается в простых кристаллах.
Взаимоотношения между частями двойника можно описать либо как отражение через плоскость, которая, за редким исключением, является возможной гранью кристалла и имеет рациональные индексы, либо как поворот на 180° вокруг оси, которая обычно (но не всегда) находится в простом взаимоотношении с кристаллографическими осями. Плоскость и ось с указанными характеристиками называются двойниковой плоскостью и двойниковой осью соответственно (или плоскостью и осью двойникования). В центросимметричных кристаллах существуют как двойниковые плоскости, так и двойниковые оси, перпендикулярные к ним. Образовавшиеся при этом двойники называются зеркальными двойниками или двойниками вращения. При стереографических построениях удобнее рассматривать двойники с точки зрения вращения. Соотношения между составными частями двойников описываются законом двойникования.
Плоскость, соединяющая две части двойника, называется плоскостью двойникового срастания (двойниковым швом). Обычно она совпадает с двойниковой плоскостью. Двойники, соединенные по четко выраженной плоскости, относятся к двойникам срастания. Однако в некоторых случаях тщательное исследование (возможное при изучении шлифов под микроскопом) показывает, что в одних случаях участки структуры с противоположной ориентацией перемежаются между собой в двух частях кристалла, а в других случаях две части кристалла, по-видимому, прорастают друг друга, образуя двойники прорастания (рис. 3.48) Их относительную ориентацию по-прежнему можно описывать с помощью двойниковой оси или двойниковой плоскости, однако плоскость срастания «растворяется» в множестве парных плоскостей решетки, пронизывающих весь объем кристалла.
Связь между двойниковой осью и плоскостью срастания в двойниках срастания создает основу для дальнейшей классификации.
Нормальные двойники имеют двойниковую ось, перпендикулярную плоскости срастания, которая является двойниковой плоскостью.
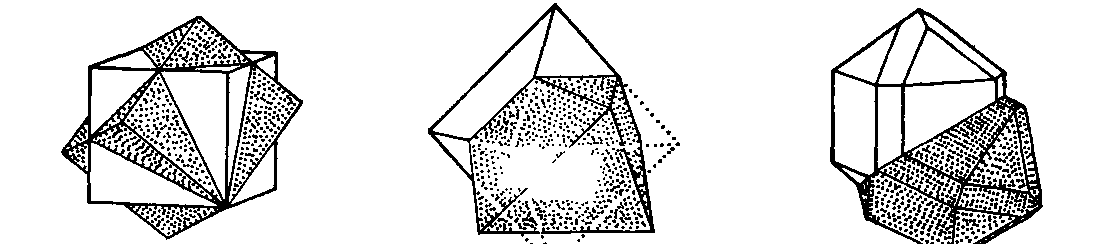

Рис. 3.48 Примеры сдвойникованных кристаллов.
Параллельные двойники содержат двойниковую ось, которая может иметь направление вдоль ребра кристалла (ось зоны) и лежать в плоскости срастания.
Сложные двойники имеют двойниковую ось, лежащую в плоскости срастания и перпендикулярную к возможному ребру кристалла.
Примеры выделенных типов двойников даны в разделе, посвященном описанию важной группы минералов — полевых шпатов.
Многократное двойникование
Процесс двойникования может повторяться в пределах одного кристалла, и при этом возможен один из двух результатов. Если двойниковые оси параллельны в последовательных элементах сдвойникованного кристалла или лежат в плоскости срастания, то образуются параллельные слои (пластинки) кристаллического вещества с обратной ориентацией, которые в совокупности составляют полисинтетические двойники.
Когда в последовательно расположенных индивидах двойниковые оси непараллельны, части двойника образуют различные многоугольные формы. Если параметры кристаллической решетки близки к тем, которые встречаются у классов с более высокой симметрией, то повторяющееся двойникование может привести к проявлению у сдвойникованного кристалла внешне более высокой симметрии. Такое миметическое двойникование (от англ, mimetic — «подражательный». — Ред.) прекрасно видно на примере арагонита (СаСОз), показанного на рис. 3.49. В данном случае в ромбическом минерале угол 110 Л 110 составляет 63° 48', что придает тройнику арагонита псевдогексагональную симметрию.
Для иллюстрации основных положений проведенного рассмотрения на рис. 3.48 показано несколько хорошо известных двойников, образцы которых легко доступны для изучения. Другие примеры даются при описании конкретных минералов.
Причины двойникования
В зависимости от генезиса различают два основных типа двойникования: двойникование роста и вторичное, подразделяемое на трансформационное и деформационное двойникования.
Рис. 3.49 Тройник арагонита: миметическое двойникование.
Двойникование роста
При описании двойникования мы основывались на представлении о вращении одной части двойника относительно другой, но в большинстве случаев такой подход использовался только для того, чтобы объяснить взаимоотношения между этими частями. Двойникование роста обычно возникает с момента зарождения кристалла, и физического вращения в действительности не происходит.
Причины двойникования в процессе роста кристаллов не вполне ясны. Кристаллы одних минералов почти всегда сдвойникованы, в то время как у других двойникование наблюдается лишь изредка или вообще отсутствует.
Разумеется, прежде всего развитию двойникования должна способствовать симметрия. Так, в гексагональной сингонии двойники встречаются довольно редко, хотя они вполне обычны в тригональной системе. В первой из них существует большое количество поворотных осей четной степени, которые, по-видимому, являются причиной такого различия. Условия для двойникования благоприятны, когда при пространственном расположении атомов в кристаллической решетке имеются плоскости или оси, по отношению к которым атомы располагаются почти симметрично. Такая ситуация наблюдается, например, у арагонита. Для иллюстрации степени несоответствия в ориентации отдельных частей двойников на рис. 3.50 показаны элементарные ячейки арагонита, наложенные на плоскость 110. Видно, что несоответствие очень невелико вдоль плоскости срастания, но становится отчетливо заметным в следующем ряду групп СОз по любую сторону от этой плоскости (рис. 3.50, a). Ha рис. 3.50(б) убраны лишние детали и можно без помех проследить любое несоответствие, следуя вдоль рядов треугольников.
Классическая теория двойникового роста подчеркивает важность минимизации внутренней энергии кристаллической решетки. Отдельный совершенный кристалл с упорядоченным пространственным расположением координационных полиэдров рассматривается как система с самым низким уровнем энергии. Двойникование, нарушая стройность такой системы, увеличивает энергию решетки. Но если ближайшие из соседних атомов по обе стороны плоскости срастания близки по своим характеристикам, то пространственное расположение анионов вокруг отдельного катиона нарушается незначительно. Тогда обратно ориентированные группы атомов, находящиеся на расстоянии от этой плоскости, большем чем длина связи, существенно не воздействуют на общую энергию решетки, и может проявиться двойникование. Независимо от этого возникновение двойников приписывается множеству нарушений на ранней стадии роста кристалла, когда, как считается, его энергетическое поле, стремящееся сохранить атомы в соответствующей ориентации, является слабым. Если происходит быстрый рост кристалла из пересыщенного раствора, то возникающие при этом нарушения роста могут зафиксироваться в форме двойника.
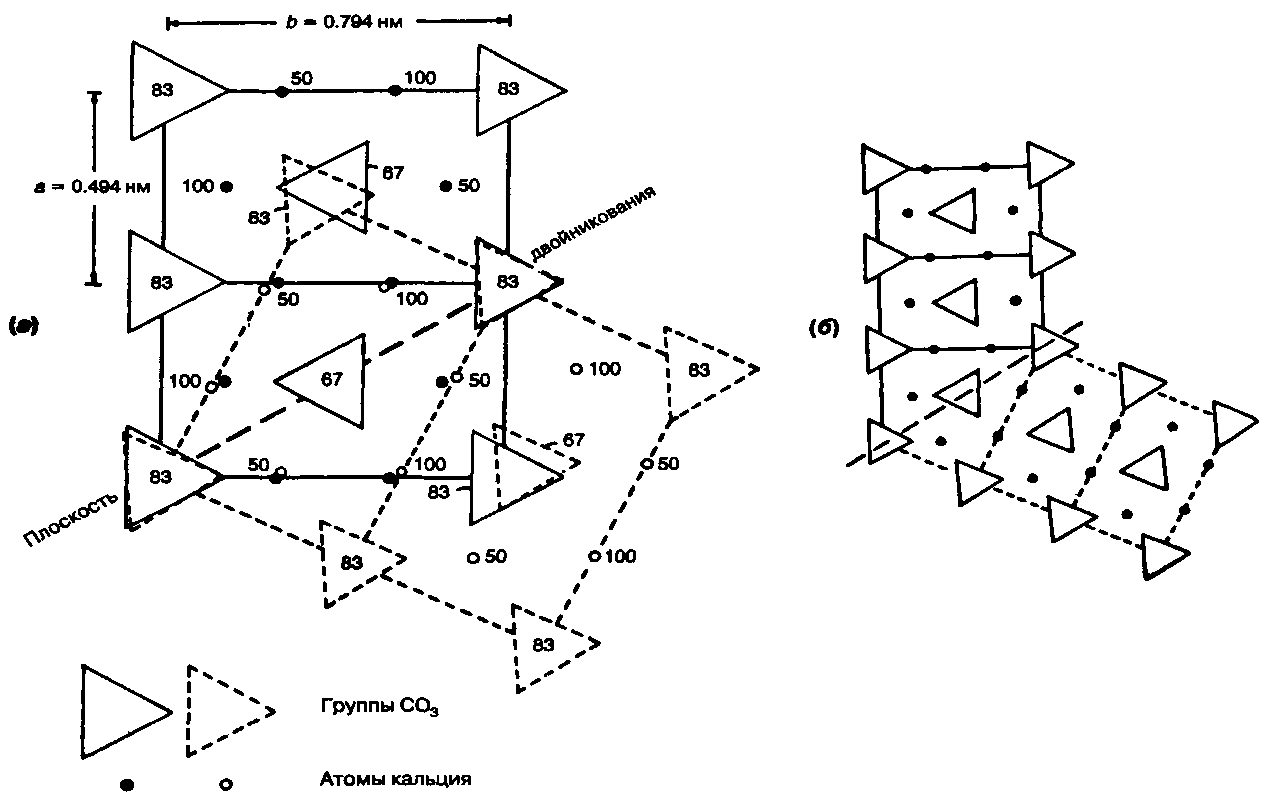
Рис. 3.50 Связь двойникования со структурой в арагоните.
Атомы кальция
Тем не менее возникновение двойников в процессе роста не ограничивается, как можно было бы предполагать, ранней стадией образования кристаллических зародышей. Например, при полисинтетическом двойниковании плагиоклазов новые пластинки с обратной ориентацией продолжают эпизодически развиваться на протяжении всего времени роста кристалла. Аналогичным образом в нарастаниях плагиоклаза на относительно крупных кристаллах-зародышах в осадочных породах двойникование проявляется независимо от его наличия в ядре. Поэтому условия, которые поддерживают возникновение обратных форм, и реакция решетки на них не полностью управляются слабыми энергетическими полями решетки, существующими на раннем этапе роста кристалла. Скажем больше — идея о том, что рост кристалла изначально направлен на минимизацию энергии решетки, мало что дает для объяснения того, почему некоторые кристаллы почти постоянно сдвойникованы.
По-видимому, существуют ситуации, когда вероятность образования большого числа обратно ориентированных форм зависит от объема атомной решетки (который должен быть близок к объему решетки с обратной ориентацией в двойнике), и тогда обратные формы могут возникать на любой стадии. Сохранение такой решетки в виде двойника зависит, вероятно, от скорости роста кристалла и поступления ионов к обеим ее частям. Многочисленные наблюдения указывают на важное значение условий роста для возникновения двойников. Имеются достаточно серьезные указания на то, что в некоторых минералах при определенных условиях двойникование происходит неизбежно. Например, плагиоклазы в изверженных породах почти всегда сдвойникованы, тогда как в породах низкой ступени метаморфизма они часто не образуют двойников. Статистические исследования дают основания полагать, что в плагиоклазах изверженных и метаморфических пород частота проявления различных законов двойникования также различна. Определенную роль помимо этого играет состав. Так, например, в обогащенном кальцием плагиоклазе из габбро толщина пластинок одной ориентации часто значительно больше, чем пластинок с противоположной ориентацией, в то время как в обогащенном натрием плагиоклазе эти два вида пластинок более близки по размерам. Следует помнить, что рост кристаллов представляет собой неравновесный процесс, часто протекающий однонаправленно в соответствии с непрерывными изменениями окружающей среды при остывании расплавов или испарении растворов. Это обстоятельство подразумевает, что условия роста и в особенности концентрация примесей, вероятно, изменяются ступенчато на протяжении небольших временных интервалов. Такие изменения могут благоприятствовать развитию плоскостных дислокаций. Более того, неправильный рост, по-видимому, будет продолжаться до тех пор, пока условия осаждения не сменятся условиями растворения.
В данной области предстоит еще многое сделать, и результаты новых исследований, по-видимому, дадут нам полезную информацию об условиях, существовавших в процессе роста кристалла.
Трансформационное двойникование
Двойникование может происходить в тех случаях, когда кристалл переходит из одной полиморфной модификации в другую в результате сдвиговых преобразований. Это двойникование позволяет ослабить напряжения, вызванные небольшими смещениями атомов при изменении симметрии. Примером может служить триклинный анортоклаз, который переходит в моноклинную форму при температурах до 7000C (температура перехода варьирует в зависимости от состава). Когда анортоклаз находится в триклинной модификации, в шлифах отчетливо видны решетчатые двойники (рисунок клетчатой ткани), образованные по двум законам — альбитовому и периклиновому, которые описаны в гл. 11. Под микроскопом можно видеть, как эти специфические рисунки исчезают при нагревании и вновь появляются при охлаждении, когда кристалл проходит через точку температурной инверсии. Размер двойниковых индивидов варьирует от субмикроскопического (определяется рентгеновскими методами) до тонких и грубых пластинок, видимых под микроскопом. Такие вариации зависят преимущественно от скорости охлаждения, которая определяет время, необходимое для того, чтобы структура кристалла пришла в соответствие с изменяющимися условиями. Этот временной отрезок называется временем нормализации.
Трансформационные двойники часто наблюдаются у низкотемпературного кварца и называются дофинейскими двойниками. Этот тип двойникования возникает в результате перехода высокотемпературного кварца в низкотемпературный, о чем говорилось в разд. 2.3.1. Происходящие при этом структурные изменения в кварце показаны на рис. 2.15. Двойниковая ось представлена кристаллографической тройной осью Z, и обе части двойника (либо левосторонние, либо правосторонние) взаимно прорастают друг друга весьма незакономерным образом. Благодаря шестерной симметрии, проявляющейся по этой оси, двойники в высокотемпературном кварце (класс 62) исчезают, если эта полиморфная модификация образуется при 5750C.
Деформационное двойникование
Если спайный выколок кальцита размером в несколько миллиметров положить на стол и надавить тупым ножом на его длинное ребро (как показано на рис. 3.51), то небольшой участок кристалла может приобрести обратный наклон по отношению к этому ребру, что приведет к двойникованию по плоскости 1102.
Двойникование такого рода, наведенное механическим воздействием, тесно связано с эффектом скольжения в кристаллах. Эти два процесса, взятые вместе, ответственны за возникновение пластического течения в кристаллических веществах, а потому чрезвычайно важны для геологии, металлургии и техники вообще.
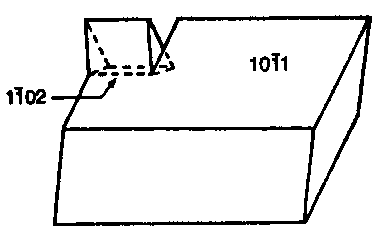
Рис. 3.51 Спайный выколок кальцита, сдвойникованный под действием давления.
Скольжение заключается в перемещении одной части кристалла относительно другой. Оно происходит по плоскостям решетки с низкими значениями индексов, и движение направлено в сторону рядов атомов с небольшими межплоскостными расстояниями. Плоскость T и направление t скольжения являются неотъемлемыми характеристиками решетки и не зависят от направления приложенной нагрузки. Степень деформации обусловлена тем, насколько благоприятно возможная плоскость скольжения ориентирована по отношению к направлению прилагаемой нагрузки. Величина сдвига вдоль каждой плоскости скольжения должна равняться сумме всех повторяющихся отрезков решетки вдоль t и может различаться в соседних плоскостях скольжения (рис. 3.52).
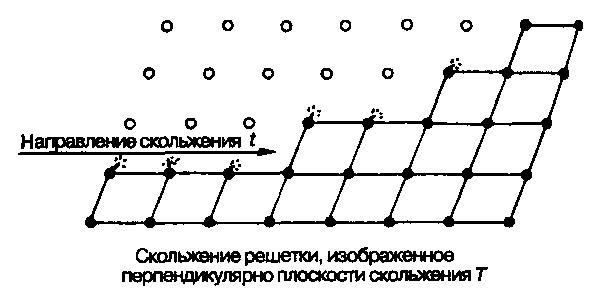
Рис. 3.52 Скольжение решетки
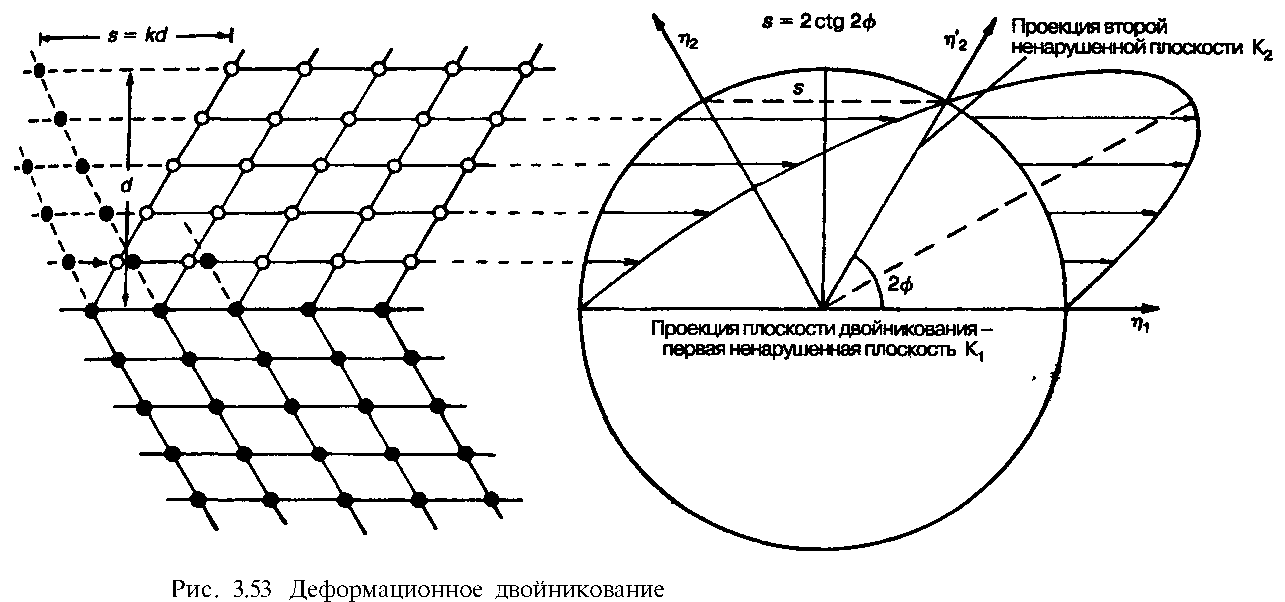
При деформационном двойниковании напряженная зона кристалла принимает двойниковую ориентацию, при которой движения по каждой плоскости в деформируемую часть кристалла, параллельную плоскости срастания, идентичны При этом величина сдвига в направлении скольжения обычно составляет только часть повторяющегося отрезка решетки. Общее расстояние, пройденное при сдвиге какой-либо плоской сеткой, пропорционально ее расстоянию от двойниковой плоскости (рис. 3.53), образующейся при однородной деформации. Если взять плоскость, расположенную под прямым углом к плоскости скольжения и сохраняющую направление движения, и нарисовать на ней круг, то в результате двойникования он превратится в эллипс. В тех местах, где этот эллипс пересекает первоначально нарисованный круг, существуют два направления п и ц2, по которым не происходит нарушений. Они соответствуют проекциям плоскостей, не подвергающихся деформациям. Первая ненарушенная плоскость Kj является двойниковой плоскостью, а вторая ненарушенная плоскость K2 находится по отношению к первой под углом, который определяет величину смещения, или скалывания. Из рис 3 53 видно, что если угол между двумя ненарушенными плоскостями обозначить через 2f, то скалывание s будет определяться формулой
S = 2ctg2f.
В общем случае любой сдвойникованный кристалл может быть охарактеризован путем определения K1 и ц2 или K2 и пг Если плоскость K1 является рациональной, то двойник можно описать как отражение через эту плоскость. Но если П представляет собой рациональное направление, то двойник рассматривается как результат поворота на 180° относительно направления скалывания Довольно часто все упомянутые характеристики являются рациональными. Зная параметры кристаллической решетки, мы можем рассчитать величину скалывания для кристалла данной толщины И наоборот, если удается выявить ненарушенные плоскости, например в случае деформированных металлов, возникают условия для установления величины перемещения в двойнике.
Смещение при скольжении рассматривается как резкий сдвиг по плоскости первичной дислокации, который осуществляется со скоростью порядка одной десятой скорости звука.
Существует также физическая теория, в значительной степени основанная на эксперименте. С ее помощью показано, каким образом перемещающиеся дислокации могут иметь компоненту, перпендикулярную начальной плоскости, и способны подниматься по спирали через последовательные решетки, что приводит к образованию однородного сдвига, характерного для деформационных двойников.
Как скольжение, так и деформационное двойникование приводят к поглощению энергии, которая обеспечивается внешней деформирующей силой. Дополнительная энергия необходима для перемещения атомов из положений с наиболее низким энергетическим запасом, которые они занимают в структуре совершенных кристаллов. По окончании скольжения атомы возвращаются на свои позиции с минимальной энергией, но внутренняя энергия системы при этом увеличивается в местах развития дефектов в кристалле. При двойниковании внутренняя энергия на двойниковой плоскости возрастает. Вероятность скольжения и деформационного двойникования зависит от энергетических характеристик атомных связей по отдельным направлениям в кристалле. Как говорилось выше, возможности проявления таких процессов наиболее благоприятны у кристаллов с металлической связью, придающей металлам ковкость. Однако деформационные двойники в металлах образуются при гораздо меньшем напряжении, чем это следует исходя из расчетов, основанных на поглощении энергии упругой деформации Теория двойникования и распространения скольжения в результате перемещения первоначальных дислокаций предназначена в том числе и для объяснения этого явления.